Полученные в предыдущем разделе результаты можно применять не только к планетам, но и к искусственным спутникам. Полная механическая энергия спутника в поле земного тяготения равна



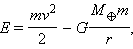
где M – масса Земли, r – расстояние до ее центра, m и v – соответственно, масса и скорость спутника. Если энергия E отрицательна, то движение будет происходить по финитной траектории – эллипсу. При круговом движении



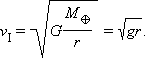
Именно такую скорость надо придать спутнику, чтобы вывести его на околоземную круговую орбиту. Если r – радиус земного шара, то получаемая по этой формуле величина называется первой космической скоростью. Она приблизительно равна 7,9 км/с.

Минимальная скорость, которую надо сообщить телу, чтобы оно никогда не вернулось на Землю, называется второй космической скоростью. Она равна параболической скорости, где r – радиус Земли:



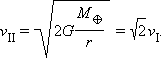
и соответствует движению по параболической траектории. Если же полная механическая энергия положительна, то спутник будет двигаться по гиперболе.

Аналогичные вычисления можно провести и для Солнца. Средняя скорость Земли относительно Солнца ~29,8 км/с. Для того, чтобы при запуске с такого расстояния тело навсегда покинуло пределы Солнечной системы, ему надо сообщить скорость относительно Солнца не меньше 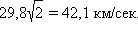. Если бы тело не подвергалось воздействию земного притяжения, то ему достаточно было бы сообщить относительно Земли дополнительную скорость 42,1 – 29,8 = 12,3 км/с в направлении ее движения. Тогда относительно Солнца тело начнет двигаться по параболической траектории. В действительности для этого требуется большая скорость, так как тело дополнительно должно преодолеть воздействие земного притяжения. Учет этой поправки дает значение 16,7 км/с. Скорость относительно Земли, которую необходимо сообщить телу, чтобы оно навсегда покинуло пределы Солнечной системы, называется третьей космической скоростью. Величина третьей космической скорости зависит от того, в каком направлении корабль выходит из зоны действия земного тяготения. Она минимальна, если это направление совпадает с направлением орбитального движения Земли вокруг Солнца, и максимальна, когда эти направления противоположны.

Если спутник, например, космическая станция, движется вокруг Земли, то космонавты внутри него находятся в невесомости. Было бы неверным считать, что сила тяжести, действующая на все тела внутри станции, равна нулю. Она отличается от силы тяжести на поверхности Земли лишь в 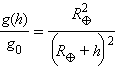раз. Т.к. высота подобных спутников h над поверхностью Земли составляет обычно сотни километров, а R = 6400 км, то сила тяжести на орбите лишь на 10–20 % меньше силы тяжести возле поверхности. Состояние невесомости на орбите создается из-за того, что спутник движется по орбите лишь под действием силы тяжести. Если рассмотреть динамику спутника в неинерциальной системе отсчета, в которой он покоится, то силе тяжести будет противодействовать равная ей по величине центробежная сила, и результирующая сила будет равна нулю.