Задачей Кеплера принято называть задачу о движении двух тел, взаимодействующих согласно закону всемирного тяготения Ньютона, с произвольно заданными начальными координатами и скоростями.
Прежде чем приступить к ее решению, необходимо напомнить некоторые факты и правила классической механики, а также объяснить общепринятую терминологию. Итак...
Действием называется величина
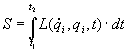 (1) (1)
где L(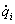 , qi,t) - некоторая скалярная функция обобщенных координат qi(i - индекс координаты), скоростей , qi,t) - некоторая скалярная функция обобщенных координат qi(i - индекс координаты), скоростей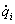 (по определению (по определению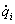 ≡ dqi/ dt) и времени t, а интегрирование ведется в интервале t1, t2. ≡ dqi/ dt) и времени t, а интегрирование ведется в интервале t1, t2.
Исходя из принципа наименьшего действия (принцип Мопертюи), который в термодинамике имеет прямой аналог - принцип минимума свободной энергии, при помощи вариации легко получаются обобщенные уравнения движения:
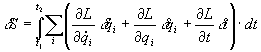
- равенство нулю вариации в целом предполагает, что равен нулю каждый из членов суммы, а это означает, что мы получаем систему уравнений, где каждое из тел для каждой из своих степеней свободы дает по одному уравнению. Так как действие есть определенный интеграл, а пределы интегрирования по времени суть константы, то вариация третьего члена суммы равна нулю. С учетом того, что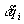 ≡ ddqi/ dt, имеем ≡ ddqi/ dt, имеем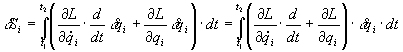 . .
Подынтегральную функцию можно проинтегрировать по частям
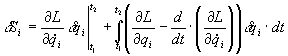
Опять же, вариация проинтегрированного члена равна нулю, следовательно, должно быть равным нулю подынтегральное выражение, откуда
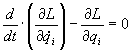 (2) (2)
Данную формулу с полным правом можно назвать обобщенными вторым законом Ньютона (как для поступательного, так и для вращательного движений).
Но для того, чтобы можно было воспользоваться полученным выражением, необходимо знать явный вид функции L(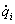 ,qi,t), которая принято назвать функции Лагранжа. ,qi,t), которая принято назвать функции Лагранжа.
В случае свободного движения тела (при отсутствии всех взаимодействий) скалярная функция получается только в одном случае: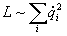 , так как при использовании любых других четных степеней вместо скаляра получается псевдоскаляр. Следовательно, , так как при использовании любых других четных степеней вместо скаляра получается псевдоскаляр. Следовательно,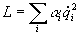 , где в случае поступательного движенияai= mi/ 2 дает определение инерционной массы тела, а в случае вращательного движения объемного телаai= Ji/ 2 - момента инерции относительно заданной оси вращения. , где в случае поступательного движенияai= mi/ 2 дает определение инерционной массы тела, а в случае вращательного движения объемного телаai= Ji/ 2 - момента инерции относительно заданной оси вращения.
Тот неоспоримый факт, что второй член уравнения движения представляет собой градиент скалярной функции, т.е. выступает в качестве обобщенной силы, позволяет в случае одномерного поступательного движения записать явный вид функции Лагранжа L=mV2/2-U(x), где функция U(x), зависящая только от координат, носит название потенциальной энергии. В случае применения формулы (2) для данного случая получаемое уравнение движения принимает вид хорошо нам знакомого из школьного курса второго закона Ньютона: m -F(x) = 0. -F(x) = 0.
В большинстве случаев получение явного вида функции Лагранжа не представляет никаких особых трудностей. Сложности возникают при попытках решения получающейся после дифференцирования системы уравнений (в декартовой системе координат это хорошо нам известная система уравнений второго закона Ньютона). Дело в том, что каждое уравнение необходимо двукратно проинтегрировать по времени, что часто бывает совсем не так легко даже в простейших случаях.
Один из стандартных методов выхода из этой проблемы - поиск какой-либо симметрии (симметрий) в полученной системе. Иногда это бывают частные симметрии, свойственные конкретной задаче; иногда - имеющие всеобщее значение.
Одну из таких всеобщих симметрий можно заметить при внимательном рассмотрении функции Лагранжа, которая никогда не зависит от времени явно, а только от координат и скоростей. Но даже явная зависимость от времени не является помехой, если не существует выделенного направления такого изменения, т.е. не появляется дополнительных компонент сил, связанных с асимметрией изменения потенциала во времени. (Подобные случаи явной зависимости потенциала от времени неизбежно приводят к зависимости сил от времени, но и только.) Следует обратить самое серьезное внимание на то, что альтернативных случаев в природе не существует. В этом (и только этом!) случае можно однократно проинтегрировать систему уравнений и получить константу интегрирования, которая определяется только начальными условиями:
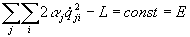 (3) (3)
где j - индекс тела, i - индекс координаты.
Эта, связанная с симметрией течения времени константа, носит название энергии системы, а ее определением служит формула (3). Для поступательного движения она может быть записана немного понятнее:
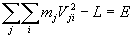 . .
Задача Кеплера есть частный случай движений в центрально-симмеричных полях, в которых потенциальная энергия является скалярной функцией только расстояния между взаимодействующими объектами. Легко доказать, что при отсутствии внешних полей, центр масс этих тел есть инерциальная система отсчета, которую удобно выбрать за начало координат. Кроме того, в решении задачи не может появиться никаких принципиально новых моментов, если допустить, что масса одного тела (которое будем считать покоящимся в центре масс) много больше массы другого - при этом изменяется только масштаб, а не форма траекторий (как результат линейной замены переменных).
Исходя из центральной симметрии, удобно записать функцию Лагранжа и энергию в полярной системе координат:
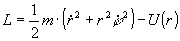 , ,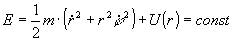 . .
Третью координату можно опустить, так как в случае выбора единственной плоскости, проходящей через центр и вектор взаимной скорости (этого всегда можно добиться вращением системы координат), координаты никогда не смогут выйти за пределы выбранной плоскости по причине отсутствия в данной задаче сил или их компонент, нормальных по отношению к этой плоскости.
Уравнение движения (2), записанное для угла, выглядит, как mr2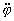 = 0, и может быть легко проинтегрировано по времени: = 0, и может быть легко проинтегрировано по времени:
mr2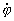 = const = M (4). = const = M (4).
Получившаяся константа M носит название момента импульса. Очевидно, что закон его сохранения верен для любых центрально-симметричных полей. Величина r2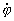 является скоростью заметания площади траектории, следовательно, уравнение (4) представляет собой немного иную формулировку II закона Кеплера. является скоростью заметания площади траектории, следовательно, уравнение (4) представляет собой немного иную формулировку II закона Кеплера.
С учетом (4) закон сохранения энергии может быть переписан:
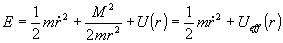 , где обозначено , где обозначено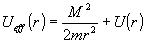 . .
Легко заметить, что для получения решения по радиусу, вместо двойного интегрирования с помощью закона сохранения энергии можно обойтись однократным:
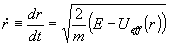 (5). (5).
Возможный минус перед корнем должен быть исключен, так как отрицательный радиус для полярной системы координат никакого физического смысла не несет.
Запись в дифференциалах (4) и (5) дает возможность исключить время и получить уравнение траектории:
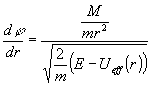 , или , или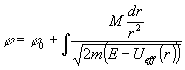 (6). (6).
Чтобы проанализировать и найти возможные траектории, необходимо воспользоваться явным видом Ueff(r). Гравитационный потенциал, исходя из закона всемирного тяготения, выглядит как U =-
a/ r (конечно же,a=gm1m2, но и этого более чем достаточно). Тогда
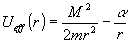 , (7) , (7)
где первый член этой формулы часто называют "центробежным потенциалом". Характерный график этой функции представлен на рисунке:
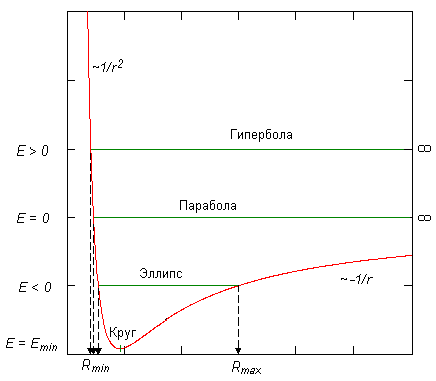
Вполне очевидно, что никаких решений ниже кривой существовать не может, так как это соответствует E< Ueff, что, в свою очередь, приводит к отрицательному значению подкоренного выражения в формуле (6). Поведение кривой объясняется довольно очевидными фактами: на малых расстояниях центробежный потенциал играет главную роль по отношению к гравитационному, так как его знаменатель зависит от квадрата расстояния от центра, но на достаточной больших расстояниях следует пренебрегать уже его влиянием из-за значительно более медленного уменьшения модуля гравитационного потенциала. Учет разных знаков приводит к характерному виду изображенной на рисунке кривой.
Следует отметить, что существовать могут только четыре принципиально отличных типа траекторий: E>0, E=0, E<0 и E=Emin. Для последнего r=const, т.е. траектория представляет собой окружность, а из закона сохранения момента импульса следует постоянная величина орбитальной скорости. Однако в природе данная траектория реализоваться не может, так как любое внешнее возмущение приведет к случаю E<0.
E>0 соответствует ситуации, когда на больших расстояниях существует заметная кинетическая энергия по сравнению с потенциальной энергией гравитационного взаимодействия, которым можно пренебречь. В этом случает траектория инфинитна (т.е. неограниченна), существует только точка минимального сближения; т.е. тела однократно сближаются и снова расходятся на бесконечность. Как это будет видно далее, данная траектория представляет собой гиперболу.
Случай E=0, соответствующий параболе, мало отличается от E>0, за исключением того, что полная энергия системы в точности равна нулю, что также является исключительным случаем, нереализуемым в природе.
И, наконец, случай E<0 - самый интересный, так как существуют как точка максимального сближения, так и точка максимального удаления (это будет соответствовать эллиптической траектории). Самостоятельно, т.е. без дополнительной энергии извне, изменить это связанное состояние тела не могут. Также без вмешательства извне невозможен и самопроизвольный переход в это состояние (некому передать излишек энергии).
И, наконец, со всей определенностью можно сказать, что падение на центр невозможно, так как этому мешает центробежный потенциал. Следовательно, столкновение объектов могут происходить только тогда, тогда точка максимального сближения меньше суммы радиусов взаимодействующих объектов. Но это достаточно редкий случай.
Теперь следует прямым способом проинтегрировать уравнение (6) с явным видом эффективного потенциала (7). Если сделать не совсем очевидную замену переменной u=1/r, то уравнение (6) примет вид:
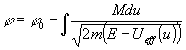
Интегрирование дает:
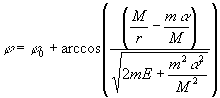
После несложных преобразований полученное уравнение можно записать как
p/r = 1 + e•cos(φ-φ0) (8)
где использованы обозначения: p = M2/mα - параметр,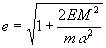 - эксцентриситет. - эксцентриситет. |



