О статье

Написана по материалам доклада, сделанного на Всероссийской астрономической конфренции ВАК-2004 "Горизонты Вселенной" (МГУ, 3-10 июня 2004 г.).

Описание базовой модели

Для создания модели движения спутников Юпитера была использована модель орбитального движения небесных тел, описанная в [1]. В данной модели движение небесного тела по эллиптической орбите разделено на движение по эллипсу (линейное) и движение вдоль радиус-вектора (радиальное). Скорость радиального движения вычисляется c использованием величины радиального ускорения, равного векторной сумме ускорения силы тяжести (a_G) и центробежного ускорения (a_C) (см. рис. 1)



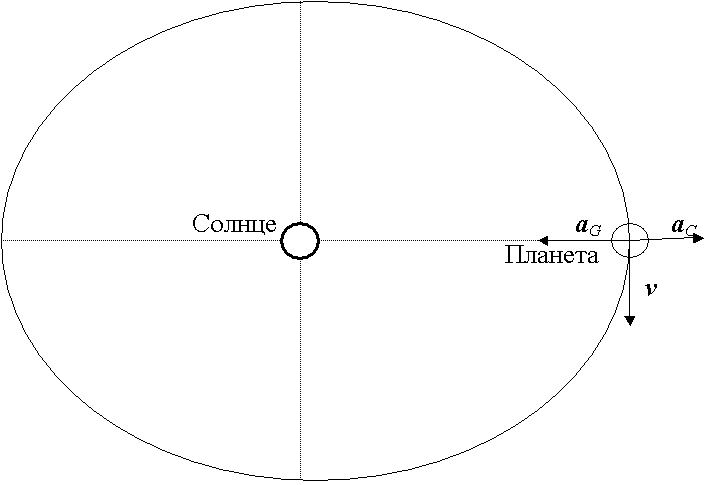
Рисунок 1. Ускорения, действующие на тело, движущееся по плоской эллиптической орбите.

a_R= a_G+ a_C. (1)

Центробежное ускорение вычисляется по уравнению [2, с. 844]:

a_C= v²/r, где: v - линейная скорость тела, r - радиус кривизны траектории.

Обе силы - притяжения и центробежная - являются центральными по определению. Поэтому их моменты относительно центра притяжения равны нулю, а величина момента количества движения тела является величиной постоянной [2, с. 438], то есть:

vr = const. (3)

Радиальное ускорение определяет скорость движение тела по оси радиус-вектора и изменение его величины (индекс «0» относится к произвольному моменту времени, принятому за начальный):

v_R(t) = v_R,0+ a_R(t)∆t (4)

r(t)=r₀+ v_R(t)∆t (5)

Исходя из вычисленного значения длины радиус-вектора могут быть получены соответствующее ему значения линейной скорости:

v(t) = v₀r₀/r(t) (6)

и ускорений.

Не смотря на свою простоту (а может быть по причине своей простоты) подобная модель не описана в доступных изданиях [3-15]. Конечно, она не обеспечивает точность, необходимую для астрономических наблюдений (см., например, [16]), но она наглядно демонстрирует, как влияют на движение тела те или иные параметры, и позволяет оценить, к чему может привести их изменение.

Результаты использования базовой модели для системы из двух тел

2.2.1. Система Солнце-Земля

Данная модель была использована для расчета орбитальных параметров Земли [1]. Вычисленный исходя из табличных значений параметров перигелия и интервала времени ∆t = 1 час. угол поворота Земли за период обращения оказался равным 359,995°, а значение радиус-вектора в перигелии отличалось от исходного на 1,4•10^-5. Расчет параметров перигелия для периода в 100 лет дал сдвиг его положения в направлении движения Земли на 4,4° по сравнению с астрометрическим значением 1,5° [17, с. 36]. При этом радиус орбиты в перигелии уменьшается до 1,468•10¹¹м (сходимость 2•10^-3), а линейная скорость движения Земли по орбите возрастает до 30346 м/с.

2.2.2. Система Солнце-Юпитер

Для расчета орбиты Юпитера было использовано несколько наборов начальных параметров. Два из них взяты из различных литературных источников [22, 23], а третий - вычислен исходя из данных, полученных с использованием программы расчета эфемерид Planeph 4.2 [24]. Собственные расчеты были сравнены с данными, полученными при использовании статистических моделей. Это уже упомянутая программа Planeph и программа Института небесной механики (The Natural Satellites Data Center (NSDC), Париж) [25]. Сопоставление различных данных приведено в таблице 1.

Таблица 1.

Сопоставление результатов расчета по различным моделям для орбиты Юпитера.

Наименование параметра	Авторская модель			Planeph 4.2	NSDC
Начальные параметры
Начальная дата	-	-	-	01.06.1904 21:00	01.06.1904 21:00
Начальная долгота, град.	0	0	0	12,40953	4,21194
Большая полуось, м•1011	7,7834б)	7,7783в)	7,7830г)	7,7830a)	Н/д
T, сут.	4332,58б)	4332,71в)	?г)	4337,92a)	Н/д
E	0,0481б)	0,0483в)	0,04823г)	0,04823a)	Н/д
Радиус, м•1011	7,40902	7,40264	7,40763	7,40760	7,40770
Угловая скорость, сек./сут.	329,74	330,13	329,42	330,13	128,2
vR, м/с	0	0	0	< 0,01	+ 0,49
Конечные параметры
Дата	-	-	-	17.04.1916 19:00	17.04.1916 19:00
Интервал, сут.	4332.583	4332,708	4337,916	4337,917	4337,917
Угол поворота, град.	359,185	360,673	360,40	360,6031	360,1692
Радиус, м•1011	7,40900	7,40261	7,40770	7,40900	7,40911
Угловая скорость, сек./сут.	329,74	329,84	329,42	329,84	?
vR, м/с	- 7,33	+ 1,83	+ 16,3	- 0,23	+ 0,24
Конечные параметры
Дата	-	-	-	11.06.2094 13:00	11.06.2094 13:00
Интервал, сут.	69406,66	69406,66	69406,66	69406,67	69406,67
Угол поворота, град.	5754,71	5781,94	5782,38	5769,986	5762,816
Радиус, м•1011	7,40888	7,43265	7,43545	7,41118	7,41129
Угловая скорость, сек./сут.	329,75	329,80	326,96	329,83	?
vR, м/с	- 34,5	+ 257	+ 247	+ 74,0	+ 74,5

Примечание:
a) Вычислено автором с использованием данных для следующего апогея (10.05.1910 20:00:00, долгота 192° 43' 13.84", радиус 8,15840•10¹¹м, угловая скорость 272,0 сек./сут., радиальная скорость< 0.01 м/с);
б) По данным [22];
в) По данным [23];
г) Взяты равными для Planeph 4.2;

Относительное расхождение между результатами, которые дают Planeph и NSDC составляет для угла поворота 0,0012 и для длин радиуса орбиты - 1,5•10^-5. Использованные в собственных расчетах исходные параметры имеют значительную вариацию: по периоду обращения - 0,0012, по угловой скорости - 0,0022, по эксцентриситету - 0,0042, по начальному радиусу лишь 9•10^-4. Сходимость между собой результатов расчетов имеет тот же порядок - на уровне 0,003. Таким образом, можно говорить о том, что точность результатов расчетов используемой модели является вполне приемлемой.

2.2.3. Система Земля-Луна

В случае системы Земля-Луна результаты расчетов оказались неудовлетворительными [1]. В качестве исходных параметров были использованы следующие значения:

- полуось орбиты - 3,844•10⁸м [17, с. 212],
- масса Земли - 5,9764•10²⁴кг [17, с. 31],
- масса Луны, равная 1/81,3 массы Земли [7, с. 62] - 7.35•10²²кг,
- сидерический период обращения Луны 27,32166 [17, с. 35],
- эксцентриситет орбиты 0,055.

Интервал времени ∆Dt = 1 минута. За время, равное сидерическому периоду обращения, Луна совершает поворот лишь на 351,85°.

2.2.4. Система Юпитер-Пасифе

Параметры орбиты Пасифе описаны в литературе недостаточно полно. Известен период обращения - 735 сут., средний радиус - 2,35•10¹⁰м (полуось 2,54•10¹⁰м), эксцентриситет - 0,38 и угол наклона орбиты к экватору планеты - 147 град. [23]. В перигее Пасифе будет обладать следующими значениями параметров:

- радиус, м = 1,5748•10¹⁰,
- линейная скорость, м/с = 3749,
- ускорение силы тяжести, м/с²= 5,11•10^-4,
- центробежное ускорение, м/с²= 8.93•10^-4,
- радиальное ускорение, м/с²= -3.82•10^-4.

Имея такое большое значение радиального ускорения тело начинает быстро удаляться от Юпитера, теряя линейную скорость, и за время, равное среднему периоду обращения, поворачивается лишь на 155 град. Параметры его орбиты при этом оказываются равны:

- радиус, м = 8,56•10¹⁰,
- линейная скорость, м/с = 689,5,
- линейное ускорение, м/с²= -5.36•10^-6,
- ускорение силы тяжести, м/с²= 1,73•10^-5,
- центробежное ускорение, м/с²= 5,55•10^-6,
- радиальное ускорение, м/с²= 1,17•10^-5,
- радиальная скорость, м/с = -665.

Тело достигнет апогея лишь через 1580 сут. имея радиус 1,083•10¹¹м и линейную скорость 545 м/с. Следующий перигей наступит через 3156 сут. с радиусом 1,574•10¹⁰м и линейной скоростью 3750 м/с, что прекрасно сходится с начальными параметрами. Но с каждым оборотом период обращения будет нарастать. Таким образом, известные орбитальные параметры Пасифе не отвечают изолированной системе Юпитер-Пасифе. Расчеты показывают, что орбита с периодом обращения 735 сут. и средним радиусом 2,35•10¹⁰м должна быть близка к круговой.

Можно полагать, что причиной данных расхождений является игнорирование влияния Солнца. Но построить модель, учитывающую влияние Солнца на основании закона Ньютона [8, с. 54]:

F_G= G•M•m/r², где: (7)

F_т- сила притяжения, M и m - массы взаимодействующих тел, r - расстояние между телами, G - гравитационная постоянная, не представляется возможным. Так сила притяжения Луны к Солнцу оказывается в два раза больше чем сила притяжения Луны к Земле. Факт обращения Луны вокруг Земли не имеет объяснения в рамках классической физики [18,19].