Волновая поверхность потенциальной энергии

Это вполне естественно, что объекты в гравитационном поле (солнце и планеты) будут стремиться занять положение с минимумом потенциальной энергии или минимумом потенциала гравитационного поля φ. Если принять такоее условие для расположения объектов на волновой поверхности гравитационного поля и учесть, что потенциальная энергия гравитационного поля каждого из объектов измеряется относительно некоторого нулевого уровня потенциальной энергии Е₀, то получаем примерно такую схему взаимного расположения объектов солнечной системы и волн, которые они создают, как показано на рис.3. Напоминаю, что волновая поверхность колебаний потенциальной энергии гравитационного поля не означает волнистость физической поверхности. Поэтому на рис.3 показано положение планет на волновой поверхности потенциальной энергии, а реальное солнце, планеты солнечной системы и их спутники будут находиться примерно в одной плоскости.



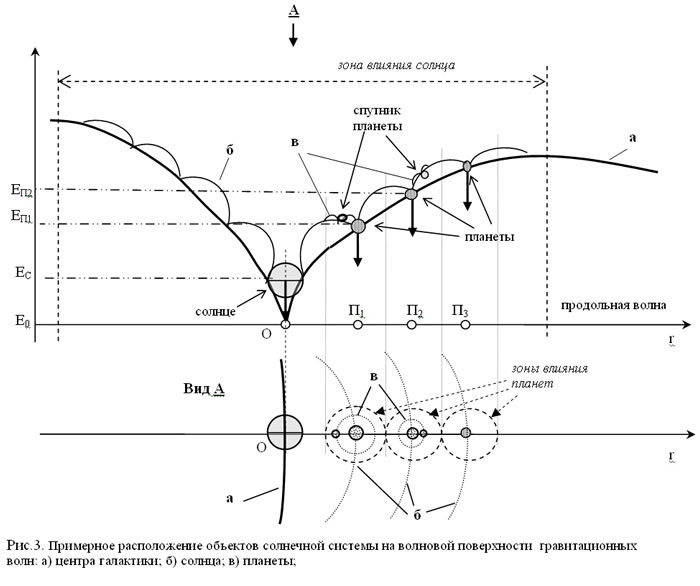
На рис.3, потенциальная энергия гравитационного поля отмечается относительно некоторой величины Е₀, принятой за нулевой уровень. У солнца, планет и их спутников будут свои уровни потенциальной энергии гравитационного поля - Е_С, Е_П1 и т.д. Хорошо видно, что планеты находятся на волновой поверхности гравитационного поля центра галактики (кривая а). Они имеет потенциальную энергию Е_п1 и Е_п2, и должны стремиться попасть в точку с меньшим потенциалом гравитационного поля П₁, П₂, П₃…- свою для каждой из планет. Этому перемещению препятствует, в первую очередь, волновая поверхность гравитационного поля центра галактики - линия а на рис.3. У  планет остается один выход - стремиться к центральному объекту (солнцу), потому что там находится ближайшая достижимая точка (точка О) с наименьшим потенциалом. Поэтому  наблюдаемая сила притяжения гравитационного поля для планет направлена к точке О. Вот откуда появилось заключение, что планеты притягиваются к солнцу. Но в природе известны случаи, когда объекты притягиваются к точкам малого потенциала при отсутствии центрального объекта - к «черным дырам», например. У них центральный объект в нашем мире отсутствует, но он все же существует. Как ни стараются планеты попасть в точку О, им это не удастся. Препятствием этому перемещению будут гравитационные волны, которые создает солнце или другой центральный объект. Поэтому просто так на солнце планета свалиться никак не сможет - для этого ей придется иметь дополнительный запас потенциальной энергии, чтобы преодолеть амплитуду колебания волны солнца. Вот так-то!

Точно так же взаимодействует система планета-спутник. Спутник будет притягиваться к точке наименьшей потенциальной энергии, которая расположена в кольце малого потенциала в окрестностях планеты, вокруг которой он вращается. На планету упасть он тоже не сможет, потому что этому препятствует гравитационная волна планеты. Ну а к солнцу спутник планеты тоже не сможет двигаться - там его ожидает еще большее препятствие! Поэтому и Луна вращается вокруг земли, не смотря на то, что сила притяжения ее солнцем (согласно закону всемирного тяготения) гораздо больше, чем землей! Оказывается, все довольно просто объясняется, если учесть действие гравитационных волн.

Такое распределение действия сил гравитационного поля недопустимо с точки зрения закона всемирного тяготения Ньютона. Однако, более общая формулировка Ньютона о силах гравитации и предлагаемая теория гравитационных волн очень хорошо согласуются между собой. Поскольку остаются в действии силы направленные к солнцу, которые заставляют планеты вращаться вокруг него. Кроме этого становится понятным, что планеты притягиваются не к солнцу - а стремятся к некоторой точке с меньшим потенциалом гравитационного поля.

Планеты располагаются в узлах колебаний гравитационного поля солнца

А теперь постараемся найти эти самые волны гравитации в космосе, и даже не очень далеко придется ходить и опытов или экспериментов никаких делать не придется. Достаточно посмотреть в справочниках или учебниках на расположение планет солнечной системы - их удаленность от солнца. Если мы будем считать расстояние в астрономических единицах (1а.е.= 149 597 870 км), а узлы колебаний расположим через 5 а.е. - это примерное расстояние между солнцем и юпитером [1,7,9], то получим примерную схему расположения больших планет солнечной системы, начиная с юпитера, которая показана на рис.4. В этом случае расстояние две полуволны или 2∙5=10 а.е. - это длина некоторого колебательного процесса гравитационного поля солнца. Исходя из закона всемирного тяготения, амплитуда колебания потенциала гравитационного поля убывает обратно пропорционально квадрату расстояния до точки измерения. Поэтому на рис.4 видно, что у гравитационной волны с удалением от ее источника мельчают кольца с малым потенциалом и соответственно мельчают и потенциальные ямы. Это означает, что чем дальше от солнца, тем меньшие объекты будут в них попадать и задерживаться, что и наблюдается на практике. Юпитер самая большая планета солнечной системы. Далее расположен сатурн - он поменьше юпитера. И чем дальше планета располагается от солнца, тем меньшие у нее размеры, эту информацию вы легко можете найти в справочниках по физике или астрономии.



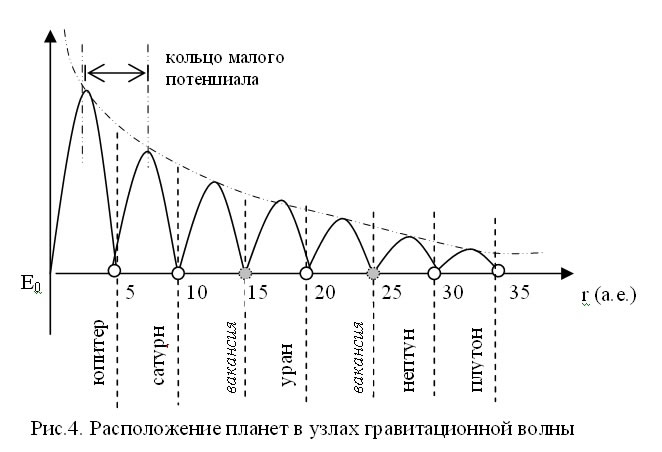
В эту схему очень хорошо укладываются планеты-гиганты солнечной системы, начиная с юпитера и дальше. На рис.4  отмечены узлы колебательного процесса гравитационного поля солнца. Напротив каждого из узлов указана планета, размер орбиты которой приближенно равен удаленности узла колебания от солнца. Как видим из рис.4, в некоторых узлах гравитационных волн нет планет видимых нам, но это не означает, что узлы остаются пустыми - в природе пустых мест не бывает. В нашем мире это просто узлы с минимумом потенциальной энергии, в которые скатываются различные астероиды, метеориты и др. Астрономы такие объекты называют «черными дырами». Правда, этот термин обычно употребляют для больших объектов типа звезды или галактики. В нашем случае для невидимых нам планет мы можем применять тот же термин «черная дыра», только у нас она будет очень малого размера. В то же время заполненные узлы очень хорошо подходят записанным в них планетам с точностью до 2-5%. Просто замечательный результат, особенно сравнивая размер солнечной системы с космическими масштабами.

И небольшое уточнение к рис.4. На нем, как видим, нашелся узел и для плутона, хотя не так давно его торжественно исключили из списка планет. Мы от плутона отказываться не будем. Даже более того, из теории гравитационных волн вытекает, что в солнечной системе должен существовать еще и восьмой узел на расстоянии примерно 40 а.е. со своей планетой - видимая она или нет еще неизвестно! А пока мы с вами будем разбираться с тем, что уже известно на сегодняшний день.

Планеты, начиная с юпитера и более удаленные от солнца, уже определились со своими узлами, посмотрим, как впишутся в эту систему планеты типа земля. Они располагаются к солнцу ближе, чем «большие» планеты, поэтому возникает вопрос о том, в каких же кольцах малого потенциала будут располагаться меньшие планеты солнечной системы. Если длина предполагаемого процесса колебаний гравитационного поля солнца равна примерно 10 а.е., то где же в этом процессе должны находиться меньшие планеты, у которых размеры орбит меньше, чем половина длины колебательного процесса гравитационного поля, которому подчиняется группа больших планет. Ведь все планеты - большие они или меньшие - должны подчиняться единому процессу колебаний, которое создает солнце.

Чтобы разобраться с этим вопросом обратимся снова к источнику колебаний. Для планет солнечной системы источником колебаний гравитационного поля, который определяет их удаленность от центрального светила, является солнце. Колебания гравитационного поля, которые оно генерирует, создали кольца малого потенциала, в которых находятся большие планеты, начиная с юпитера. Значит, солнце можно считать генератором волн. А что такое генератор колебаний, и какие его свойства?

На данный момент довольно хорошо изучены генераторы электромагнитных колебаний [2,3]. Все они состоят из физических элементов. Основным элементом генератора электромагнитных колебаний может служить некоторый электронный прибор, например, ламповый или полупроводниковый, может использоваться кварц и т.д. Все они создают колебания электромагнитного поля. Генератора, который бы генерировал только одну единственную частоту или длину волны в природе не существует, потому что все они реальные элементы, а не идеальные, и генерируют хоть и довольно узкую, но все-таки полосу частот. Поэтому для каждого генератора есть длина волны или частота, которую назначают основной, но чтобы ее получить обязательно устанавливается целая система фильтров. Кроме этого каждый генератор обязательно генерирует и гармоники - это колебания, частота которых в 2, 3, 4, и т.д. раз больше основной. Соответственно длина волны гармоники будет в 2, 3, 4… раза меньше, чем у основного колебания. Они так и называются - вторая гармоника, третья гармоника, четвертая и т.д. Правда, амплитуда гармоник значительно меньше, чем у основной частоты и убывает с ростом номера гармоники. Определять амплитуду гармоники, зная амплитуду основного колебания, математики умеют уже давно. Для того существуют методы разложения функций в ряд Фурье, Лагранжа и т.д. [3,8] Поскольку у реальных генераторов существуют гармоники, то почему бы им не быть и у реального генератора колебаний гравитационного поля - солнца. Правда, у генераторов электромагнитных колебаний ненужные гармоники подавляются при помощи всевозможных фильтров, а у солнца, свободно перемещающегося в гравитационном поле, таких фильтров пока не наблюдается, поэтому гармоники должны быть обязательно.

Итак, имеем солнце - это реальный генератор колебаний (гравитационного поля). Мы нашли кольца малого потенциала, которые создаются колебаниями основной его частоты. В узлах этого колебания располагаются планеты солнечной системы, начиная с юпитера. Как реальный генератор оно должно генерировать кроме основного колебания и высшие гармоники. Поэтому меньшие планеты солнечной системы, которые располагаются к солнцу ближе, чем юпитер, мы с вами будем искать как результат действия гармоник основного колебания. Поскольку гармоники имеют не только меньшую длину волны, но и меньшую амплитуду, чем у основного колебания, то нам стоит обратить внимание только на первые узлы высших гармоник, где амплитуда еще сравнительно велика.

Первый узел основной гармоники находится на расстоянии 5а.е., посчитаем, на каком расстоянии будут находиться первые узлы высших гармоник (для этого 5 а.е. надо делить на 2, 3, 4, и т.д.) и запишем результат в таблицу. Вставим планеты в соответствующие ячейки, результат запишем в табл. 1 (пустые ячейки пропущены).

Таблица 1. Расчет удаленности первого узла высших гармоник

Узел 1-ой полуволны высших гармоник	Расст. от солнца (а.е.) (расчетное)	Планета	Малая п/ось (а.е.) (расчетное)	Большая полуось (а.е.) [7]
Вторая гармоника	2,5	Астероиды		2,8
Третья  гармоника	1,67	Марс	1,517	1,524
Пятая  гармоника	1	Земля	1	1
Седьмая  гармоника	0,715	Венера	0,723	0,723
Тринадцатая  гарм.	0,379	Меркурий	0,38	0,387

Как видно из таблицы 1, все меньшие планеты типа земля очень хорошо уложились каждая в свою ячейку - в свою гармонику, даже нашлось место и для пояса астероидов. Все это наглядно можно рассмотреть на рис.5. Только вот примечательная вещь - планеты типа земля все принадлежат только нечетным гармоникам - в кольцах четных гармоник планет не существует. Этот момент необходимо отметить, он нам пригодится для прояснения еще одного феномена нашей солнечной системы.



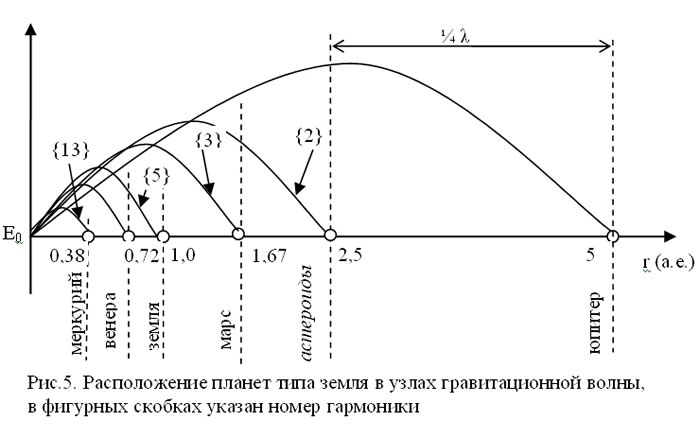
Факт, что все планеты солнечной системы располагаются в узлах нечетных гармоник, указывает на то, что математическое описание гравитационных волн солнца представляет собой нечетную функцию, у которой не может существовать четных гармоник [2,7]! Поэтому никакой планеты между марсом и юпитером ни в коем случае существовать не может. Т.е. никаких космических катастроф с гибелью мифической планеты не было, и быть не могло! А наличие на этой орбите пояса астероидов указывает на то, что солнце генерирует не одну частоту (как идеальный элемент) а некоторую полосу очень близких по частоте колебаний, что вполне естественно для природного явления. Учитывая это можно предположить, что возможно существование и 4-ой гармоники основного колебания гравитационной волны солнца. Располагаться она должна между марсом и землей и представлять собой пояс метеоритов - и то не очень крупных, - сведений о таком поясе в учебниках нет, но такое явление может иметь место.

Формирование орбит планет волнами гравитации

Как видите, с помощью теории гравитационных волн удалось объяснить довольно много. Только что мы с вами выяснили, от чего зависит удаленность орбит планет. Но и формы орбиты у планет таят также некоторые загадки, которые попробуем прояснить с помощью теории волн гравитационного поля. Для чего опять обращаемся к учебнику астрономии и вспоминаем, что известно о формировании орбит планет. А ничего неизвестно, только лишь на основе многолетних наблюдений за планетами  констатируется, что орбиты планет своей формой напоминают эллипс, при этом солнце должно находиться в одном из его фокусов [1,6,7]. Так гласит первый закон Кеплера. Схематически это выглядит примерно как на рис.6а.



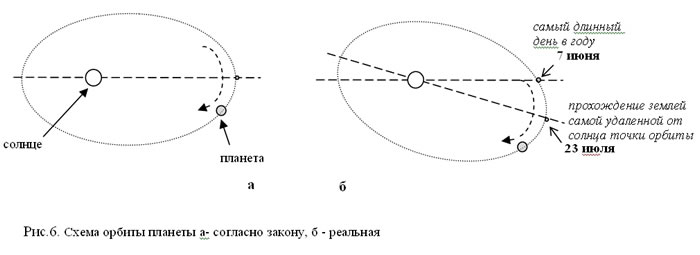
Если придерживаться этого закона большая полуось эллипса орбиты должна соединять точки самого большего и самого меньшего удаления планеты от солнца. Логично предположить, что точки пересечения большой полуоси с орбитой планеты должны отмечать также точки самого длинного и самого короткого дня года (рис.6а). Однако на самом деле последнее условие не выполняется.  Потому что наша планета, например, проходит точку самого продолжительно дня 7 июня, а самую удаленную от солнца точку орбиты - афелий наша планета проходит 23 июля [7] (рис.6б). Почему именно так и не иначе? А никто не объясняет! Кроме того возникают сомнения, что солнце останется на линии большой оси эллипса орбиты Значит, и с этим законом что-то не так!  К тому же существуют таблицы поправок положения планет свои для каждого года - это значит, что форма орбиты планеты также отличается от эллиптической. А какая же она на самом деле?..  

Ну а теперь посмотрим, что получится с орбитами планет с учетом гравитационных волн. На рис.7 можно проследить, как распространяются продольные и поперечные гравитационные волны. Продольные волны распространяются вдоль радиуса от источника гравитационных волн. Например, продольная гравитационная волна, сформированная солнцем, распространяется от солнца к планетам, а продольные гравитационные волны планет распространяются вдоль радиуса, соединяющего точку в ее окрестностях с планетой. Поперечные волны распространяются перпендикулярно продольным волнам. Поэтому поперечные волны гравитационного поля солнца распространяются вдоль окружностей, удаленных на расстояние r от солнца. Солнце в свою очередь вращается вокруг центра галактики и находится на волновой поверхности созданной колебаниями гравитационного поля центра нашей галактики. У центра галактики также можно выделить продольные и поперечные гравитационные волны - они управляют перемещением солнца вокруг центра галактики. Кроме того, они формируют орбиты планет солнечной системы. Чтобы убедиться в этом рассмотрим схему на рис.7.



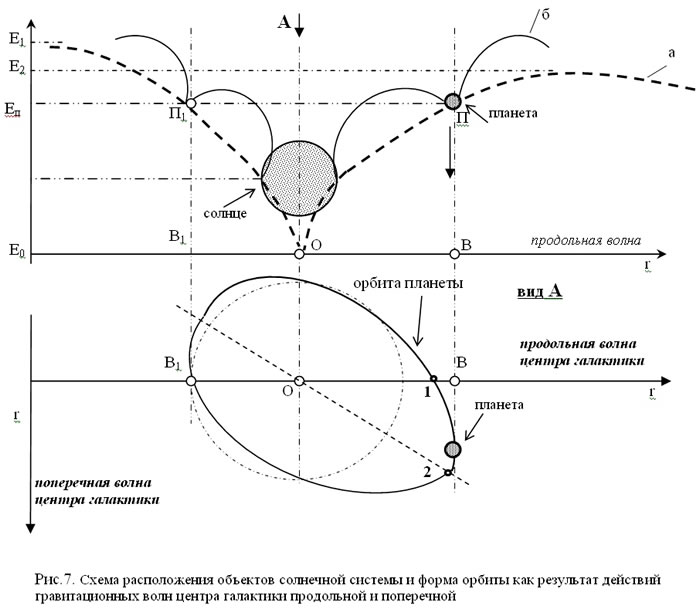
Прошу обратить внимание, что две соседние полуволны колебаний волновой поверхности гравитационного поля, в общем случае, всегда будут иметь разную амплитуду колебания. На рис.7 две соседние продольные полуволны имеют амплитуды колебания потенциальной энергии Е₁ и Е₂. Вызывается это тем, что сила воздействия гравитационного поля убывает обратно пропорционально квадрату расстояния от источника - в нашем случае от источника гравитационных волн - центра галактики. Это общее правило для процессов распространения чего-либо в пространстве [6]. Для идеальных колебаний этого достаточно, а в реальных условиях будет добавляться еще и естественное затухание - убывание силы действия в зависимости от параметров среды, в которой происходит распространение колебаний - потери при распространении. Естественное затухание определяется параметром, который называется добротностью системы. Чем выше добротность системы, тем меньше затухание. Для простоты будем считать, что затухания колебаний не существует.

Из-за того, что соседние полуволны гравитационного поля будут иметь разную амплитуду, они будут иметь разную крутизну возрастания параметра. Поэтому у двух точек с одинаковой величиной измеряемого параметра, например П и П₁, но лежащих на соседних полуволнах будет разное расстояние до точки с наименьшим параметром или точкой нулевого уровня: ВО≠В₁О. Если бы амплитуды параметра были одинаковыми у всех полуволн, то орбита планеты была бы правильной окружностью. А потому что амплитуды разные, то орбиты планет из круговых превращаются в некоторые овалы. При этом центральный объект будет находиться не в центре овала, а смещен в сторону полуволн с большим потенциалом. И это еще не все. Из-за разной крутизны возрастания амплитуды параметра, часть овала образованная полуволнами с большей амплитудой будет шире, а часть овала, образованная меньшими полуволнами - более узкая (см. рис.7, вид А).

Значит, орбита планеты должна напоминать по форме не окружность, и даже не эллипс, а контур геоида, или попросту говоря - яйца. Хотя, как уже упоминалось, согласно первому закону Кеплера планеты движутся по эллипсам, в одном из фокусов которого находится солнце. Имеют ли орбиты планет форму геоида, а не эллипса - это скажут специалисты. Но вот точно известно, что земля имеет форму геоида [4]. Солнце тоже имеет форму геоида [7]. Яйца птиц тоже имеют такую же форму. А теперь мы с вами знаем причину появления таких форм в природе - во всем виноваты гравитационные волны. Большие или маленькие, но это они действуют везде и везде искажают идеальную сферическую форму, превращая предметы или объекты, которые теоретически должны быть круглыми, в геоиды.

Из-за того, что будет убывать амплитуда и продольной гравитационной волны и поперечной волны, то ось получающегося овала орбиты планеты никогда не будет совпадать с направлением распространения ни одной из волн гравитационного поля. По определению продольная волна - это упругая волна сжатия, которая распространяется от источника колебаний. Поэтому она действует всегда вдоль линии, которая соединяет источник колебания и объект, который находится в кольце малого потенциала этого колебания. Т.е. направление распространения продольной волны - это линия, соединяющая источник гравитационной волны и меньший объект. На рис.7 линия Е₀О - это линия распространения продольной гравитационной волны центра галактики. А точка 1 на орбите планеты - это точка летнего солнцестояния, когда день на планете (в частности на земле) будет самый длинный в году. Кроме этого существует еще одна характеристическая точка орбиты, которая называется афелием, это точка 2, когда планета находится на самом большом удалении от центрального объекта - солнца. Так вот, если орбита формируется гравитационными волнами (продольной и поперечной одновременно) эти две точки орбиты - точка 1 летнего солнцестояния и точка 2 афелия - никогда не будут совпадать. Для нашей планеты это условие соблюдается. Потому что летнее солнцестояние у нас - это 7 июня, а афелий наша планета проходит 23 июля. Точно так же не совпадают точка перигелия (когда планета находится к солнцу ближе всего) и точка зимнего солнцестояния, когда день самый короткий [7]. Так что мы с вами нашли подтверждение правильности наших рассуждении о влиянии гравитационных волн на форму объектов и их орбит, и нашли объяснение ориентирования осей орбит планет, как и любых других объектов, в пространстве.



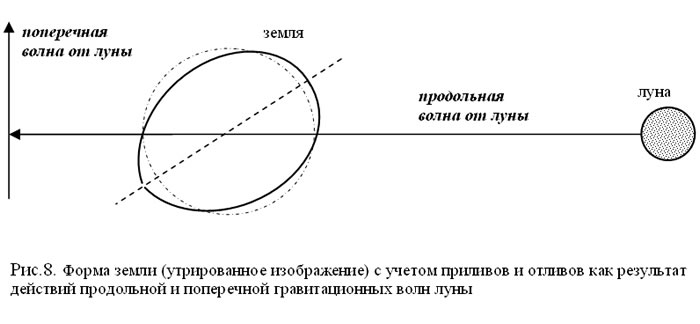
Еще один пример изменения формы объекта вследствие действия гравитационных волн можно увидеть на примере приливов и отливов на нашей планете земля под действием сил притяжения луны. Для идеального случая максимум приливной волны, учитывая закон всемирного тяготения, всегда должен быть на одной линии, связывающей центры луны и земли. Однако в реальности существует некоторое опережение максимума приливного выступа на земле по сравнению с движением самой луны. Он составляет сравнительно большую величину - угол порядка 2-4°. Изменение формы земли под действием приливных сил утрированно показано на рис.8. Такая большая величина - 2-4°  объясняется  в учебниках неким «приливным трением», что несколько сомнительно, потому что это составляет примерно 400 км! Не многовато ли? Но если мы посмотрим на эту картинку с точки зрения гравитационных волн, то становится понятным, что форма земли с учетом действия двух ортогональных волн гравитационного поля луны должна! иметь именно такую форму и никакую другую. И максимум «приливного» выступа ни в коем случае не должен совпадать с линией центров масс земли и луны. И приливное трение тут вовсе не причем. А то, что мы называем приливами, на самом деле действие гравитационных волн луны (продольной и поперечной), которые заставляют местами сжиматься, а местами вытягиваться нашу планету по всей ее толщине. Точно так, как изменяется орбита планеты под действием гравитационных волн центра галактики, точно так же изменяется форма нашей планеты по широте (приливы) под действием гравитационных волн нашей соседки луны.

Еще под это правило подпадает форма орбиты луны. Астрономы просчитывают орбиту луны при ее вращении вокруг земли с учетом силы притяжения ее землей, а потом вводят поправки к ее орбите (они называются возмущениями орбиты), которые учитывают влияние силы притяжения луны солнцем. Это вполне логично. И расчеты вполне подтверждаются наблюдениями. Только данные для расчетов не совсем логичные. Сначала факты:

1) расстояние от солнца до земли составляет примерно 1 а.е.;

2) расстояние от земли до луны - примерно 0,2 а.е.

При расчетах этих возмущений основными параметрами является масса солнца и луны, что вполне естественно, и некоторое расстояние. Вопрос к вам: - какое расстояние берется при расчете возмущений орбиты луны, вызванных влиянием гравитационного поля солнца?

- Может быть 1,2 а.е. - самое большее удаление луны от солнца?

- Или может быть 0,8 а.е. самое меньшее удаление луны от солнца?

- Может быть 1 а.е., в конце концов, - средняя величина? Ни первое, ни второе и ни третье.

Это все неправильные ответы. Оказывается при расчете возмущений орбиты луны, вызванных влиянием гравитационного поля солнца, берется величина 0,2 а.е. [1] - расстояние от луны до земли! Почему так, а не иначе, астрономия не объясняет, просто констатирует.

А вот с точки зрения волновой теории все это объясняется довольно просто. Луна находится в том же кольце малого потенциала, что и земля. Земля как более массивный объект занимает центральное положение в области этого кольца с самым малым потенциалом в этом кольце. Луна находится на расстоянии 0,2 а.е. от земли и от точки наименьшей потенциальной энергии кольца, примерно в которой находится земля. Солнце своей гравитационной силой воздействует на луну. Но его воздействие заключается не в том, чтобы притянуть луну к себе ближе, как того требует закон всемирного тяготения, - нет! Воздействие гравитационных сил солнца, а точнее колебание его гравитационного поля направлено на то, чтобы луну столкнуть в центр потенциальной ямы, где уже находится земля. Поэтому и величина возмущения от воздействия гравитации солнца на луну будет рассчитываться из расчета 0,2 а.е., которых не хватает, чтобы она попала в ту же точку, что и земля. Так что все просто и понятно, если посмотреть на возмущения движения луны с точки зрения волновой теории.

Загадка орбиты меркурия решается просто

В этой работе вы познакомились с теорией гравитационных волн. Это абсолютно новая теория, которая в таком виде еще нигде не представлялась. Она помогает раскрывать причины многих явлений гравитации и не только гравитации. Теорий по разделу гравитации в физики не так уж и много. Они помогали объяснить многие явления, особенно связанные с дальним космосом и ближним тоже. Но пока еще ни одна из теорий не решила загадки орбиты меркурия. Даже общая теория относительности А. Эйнштейна с ее мощнейшим математическим аппаратом не смогла подобрать ключик к этой загадке. А ведь меркурий уже давно смущает умы всех ученых, которые изучают гравитацию и механику движения планет. Дело в том, что перигелий меркурия прецессирует, т.е. смещается, из-за чего его орбита не замкнутая. Т.е. орбита меркурия - это не замкнутое кольцо, как считается для других планет, а представляет собой незамкнутый овал, когда несколько оборотов планеты вокруг солнца  описывают лепестки некоей спирали, у которой минимально удаленная от солнца точка (перигелий) описывает дугу. За сто лет наблюдений перигелий орбиты меркурия сместился примерно на 42 угловых секунды [6]. С одной стороны это величина не очень большая, но с другой стороны, хотелось бы знать, какие скрытые силы возмущают его орбиту.

Что-то у меркурия происходит не так как у остальных планет. Чтобы понять, в чем кроется причина этого явления, поищем, чем отличается меркурий от других планет солнечной системы. Отличие есть и значительное - это большой эксцентриситет (разница размеров большой и малой осей орбиты планеты). У плутона он тоже большой, только вращается он гораздо медленнее, чем меркурий, поэтому, наверное, странностей его орбиты не успели отметить - это еще впереди.

Первый вопрос, который возникает - это вопрос о причине возникновения таких больших эксцентриситетов. Ответ, как обычно, отыскивается в волновой теории гравитации. Вспомните, что меркурий самая ближняя, а плутон - самая дальняя из планет солнечной системы. Меркурий - это тринадцатая гармоника гравитационной волны солнца, а плутон - 7-ой узел гравитационной волны солнца. У них у обоих амплитуда гравитационной волны солнца уже будет уже довольно мала: у первого из-за большого номера гармоники, у второго из-за большой удаленности от солнца. Поэтому при формировании ширины их орбиты или кольца малого потенциала начинает сказываться влияние изменения амплитуды гравитационной волны центра галактики. Это может происходить, когда изменения амплитуд близлежащих полуволн солнца и соответствующий им перепад амплитуды колебания волны центра галактики, сравнимы по величине. В таких случаях ширина кольца малого потенциала может увеличиться на 2, 3 и т.д. гравитационных волн.

Итак, обычные планеты перемещаются по своим орбитам в кольцах малого потенциала. Ширина минимального кольца для планет типа земля составляет примерно диаметр планеты d. Это значит, что между внутренним и внешним кольцом орбиты планеты существует разница в d, а если вести отсчет вращения по центру планеты - разница составит ½d. Из-за несовпадения количества волн внешнего кольца орбиты и внутреннего, орбиты планет никогда не будут замкнутыми, и за каждый оборот планеты вокруг светила будет происходить смещение перигелия планеты на ½d. Для земли это соответствует ¼ суток. На сравнительно небольших промежутках времени это смещение также сказывается, и заметить это можно только с помощью очень точных приборов. Чтобы убрать погрешность из-за разницы длин волн внешней и внутренней границ орбиты, в наш календарь периодически вводятся дополнительные правки - большие или маленькие. Например, последняя большая правка вносилась в 1582 году, реформой папы Григория XIII переносилась дата на 10 дней вперед [7]. А последняя - очень маленькая правка вносилась в конце 2005 года - изменение составляло всего лишь 1 секунду. Т.е. постоянно проводятся необходимые корректировки для соответствия положения земли на орбите и отсчитываемых периодов - лет.

Далее, обычно у планет небольшая величина эксцентриситета и они не уходят из своего кольца малого потенциала колебаний (см. рис.9а), поэтому таких правок бывает достаточно. С меркурием дело обстоит несколько иначе. Из-за большого эксцентриситета е=0,2 орбиты меркурия [1,7,9], его перигелий отличается от афелия на величину 2ае, где а - это большая полуось орбиты. Значит, различие составит 2*а*е = 2*0,387*149,6*0,2≈23 тыс. км. Эта величина составляет почти 5 диаметров планеты. В этом случае общая толщина кольца малого потенциала в афелии составит 5+1=6 (рис.9б) или 6d.



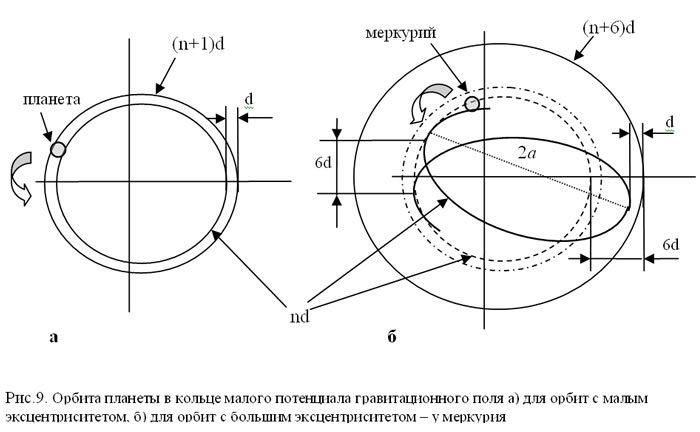
Поэтому толщина кольца малого потенциала у меркурия в афелии увеличилась на 6 диметров. А это значит, что для сохранения количества поперечных волн в кольце малого потенциала орбиты пойдет смещение положения перигелия орбиты меркурия относительно предыдущего на 6 диметров, что составит 6*4,9 = 27,6 тыс. км.

Если протяженность орбиты меркурия составляет примерно 2πа (а - большая полуось орбиты) или 364 млн. км, что составляет 360° или 360*60*60 угловых секунд, то 27,6 тыс. км за один оборот меркурия вокруг солнца составят примерно 0,098 угловых секунды. А за 100 лет наблюдений меркурий сделает примерно 415 оборотов вокруг солнца. Поэтому общее смещение перигелия за это время составит по ориентировочным расчетам 41 угловую секунду. Напомню, что астрономические наблюдения за орбитой меркурия показали, что смещение за 100 лет наблюдений составило примерно 42 угловых секунды, для сравнения мы насчитали 41 угловую секунду. Ну что же для наших приблизительных расчетов этот результат можно считать просто замечательным. Напоминаю, что все наши вычисления были приблизительными и все равно мы получили результат очень близкий к наблюдаемому смещению перигелия меркурия. Это показывает, что с точки зрения волновой теории гравитационного поля проблема смещения перигелия орбиты меркурия вполне разрешима.

Как видите, теория гравитационных волн справилась и с загадкой смещения орбиты меркурия, что подтверждает действенность этой теории при решении задач небесной механики. Но она же решает и многие другие задачи - даже задачи управления гравитацией вообще.

Список литературы
1. Бакулин П.И., Кононович Э.В., Мороз В.И., Курс общей астрономии. М., Наука, 1983г.
2. Баскаков С.И., Радиотехнические цепи и сигналы. М., Высшая школа, 1988г.
3. Гавриленко Н.И., Радиопередающие устройства. М., Транспорт, 1983г.
4. Жарков В.Н., Внутреннее строение Земли и планет. М., Наука, 1983г.
5. Иваненко Д.Д. Актуальность теории гравитации Эйнштейна. Сборник «Проблемы физики: классика и современность», М., Наука, 1982г.
6. Ч.Киттель, У. Найт, М.Рудерман, Берклеевский курс физики., т.1, Механика. М., Наука, 1975г.
7. Кононович Э.В., Мороз В.И., Курс общей астрономии. М. изд-во Едиториал УРСС, 2004г.
8. Г.Корн, Т.Корн, Справочник по математике для научных работников и инженеров, М. Наука, 1974г.
9. Кошкин Н.И., Ширкевич М.Г., Справочник по элементарной физике. М., Наука, 1988г.
10. Попов И.Ф. Стационарные волны гравитации в управлении космосом, ISSN 0869-6772, Конверсия в машиностроении, 2005г. №1-2
11. Трофимова Т.И., Курс физики, М., Высшая школа, 1985г.
Инна Павловна Бабич, адрес для почты E-mail: innapavlovna@list.ru, образование высшее - радиоинженер, закончила Харьковский авиационный институт.