Смещение Доплера в гравитационном поле

Для определения лучевой скорости звезды используется метод измерения смещения Доплера. Длина волны воспринимаемого излучения сокращается или увеличивается в зависимости от движения излучающего или отражающего свет объекта по лучу зрения относительно наблюдателя.



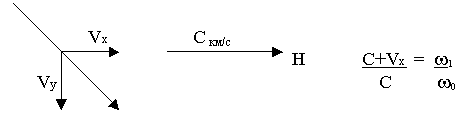
Изменения частоты мы оцениваем как реально существующую скорость Vx, а скорость Vy и Vz мы наблюдаем по смещению звезды на небосводе, так строится вектор движения.

Смещение Доплера является хорошей "линейкой", современные приборы дают погрешность не более 0,1 км/с. По результатам измерений строятся орбиты движения, изучаются процессы происходящие внутри звезд, и на основании красного смещения удаленных галактик сделан вывод о первоначальности материи, так называемый "Большой взрыв".

Предлагаю Вашему вниманию способ доказать, что взаимосвязь "частота - лучевая скорость" верна только при прямолинейном и равномерном движении излучающего или отражающего свет объекта, а если на объект в момент излучения действовала сила и он испытывал ускорение, то смещение Доплера не соответствует реальной лучевой скорости, но находится с ней в непосредственной взаимосвязи.

Для анализа предлагаю представить некоторое тело двигающееся по окружности с радиусом R относительно центра О с орбитальной скоростью V.



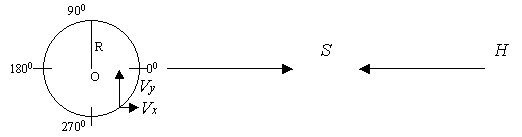
Наблюдатель находится на расстоянии S от центра окружности. Допустим, что в какой-то момент времени на этом двигающимся объекте производится некоторое количество (n) выстрелов за 1 сек. в сторону наблюдателя, наблюдатель может наблюдать также и световые вспышки от этих выстрелов. Рассмотрим в какой последовательности свет от вспышек и пули достигнут наблюдателя.

I. В случае со вспышками (свет от первой и последней вспышки должен двигаться до наблюдателя с одинаковой скоростью и через какой-то момент времени свет дойдет до наблюдателя, но так как тело двигалось по окружности и имело относительно наблюдателя скорость Vx, то между первой и последней вспышкой существуетDX = sinAV•1 сек., след, время за которое наблюдатель увидит n ( количество) вспышек изменится на время

Δ t = sin α V • 1сек/C

, частота излучения при вспышках тоже изменится и будет

ω^I/ω₀= 1сек + Δ t / 1сек

Так измеряется лучевая скорость Vx:

Vx=Vx₀+ sinAV

где Vх₀- скорость по оси Х между наблюдателем и центром окружности;
V - скорость движения по орбите;
A- угол между лучом зрения и орбитальным положением источника.

II. В случае с пулями ситуация будет другая. Допустим, что в течение всего времени полета пуля имеет равномерное и прямолинейное движение относительно стрелка. Так как стрелок находится на теле, которое движется по некоторой окружности с радиусом R, то до наблюдателя первая и последняя пуля будут лететь с разной скоростью, так как Vx относительно наблюдателя изменилась:

DV_x= cosA•A•t = cosA(V²/R)•1 сек

a = (V²/R) - ускорение с которым двигается тело.

Каждую секунду расстояние между пулями изменяется наDx =DVх•1 сек. и хотя скорость полета первой и последней пули примерно одинакова и равна

С¹= С + V_х0+ sinAV , то расстояние между первой и последней пулей изменяется:

l₀= (C + sinAV)•1 сек



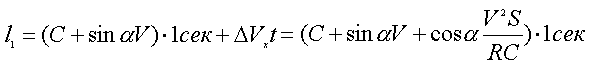
где а = (V²/R) - ускорение;
S - расстояние от наблюдателя до объекта;
С - скорость движения пули;
S/C - время, за которое пуля летит до наблюдателя.

Допустим, что свет от вспышек мы не видели вовсе, не измеряли действительной скорости пули, а просто замерили время, за которое в мишень ударилось n-количество пуль, допустим это 1,1 сек. Может или нет наблюдатель оценить скорость Vх объекта.

Если бы движение объекта было равномерное и прямолинейное, тогда

cosα (V²S/RC) = 0

и тогда мы могли бы смело утверждать что

V_x= 0.1 C

, но так как тело испытывало ускорение, то для решения можно предложить неограниченное количество орбит, по которым может двигаться тело, на котором находился стрелок, а значит частота с которой приходят пули от выстрелов не может являться свидетельством реальной скорости объекта по лучу зрения.

Теперь предлагаю проверить имеем или нет мы право называть свет волной, распространяющейся относительно наблюдателя и источника всегда с одинаковой скоростью, независимо имеет ли источник движение и/или ускорение по оси Х (лучу зрения) или не имеет. Изменение нашей оценки очень существенно для астрономии.

Итак: вариант I.
Свет относительно наблюдателя и/или источника двигается всегда с постоянной скоростью С, а измеряемая лучевая скорость (Vх) равна : V_x=V_ox+ sinAV , так как



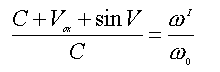
Вариант II.
Свет распространяется с постоянной скоростью относительно источника, а для наблюдателя скорость приходящего излучения (С^I= С + sinAV). Тогда измеряемая лучевая скорость будет:



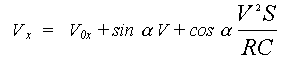
где V^х- скорость движения по оси Х центра вращения или наблюдателя,
V - скорость движения излучающего или отражающего свет тела по орбите,
S - расстояние до наблюдателя,
R - радиус орбиты по которой движется тело,
С - скорость света.

Эта формула может выглядеть и по другому, если ввести t_об

t_об= 2π•R/V , R = t_об•V/2π

тогда



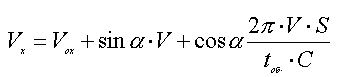
Между реально существующей и измеряемой лучевой скоростью существует разница



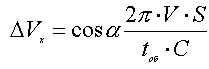
, так как S/C - расстояние до объекта в свет, тогда

V^I_x= cosα•6.28•V•расстояние в свет.годах/время оборота выраженное в годах

где V^I_x- поправочная или измеряемая скорость, V-скорость движения по орбите
V^I=V_измер.- V_{расчет.}

Идеальным объектом для проверки служит спутник Юпитера Амальтея:
Расстояние до центра планеты R = 182 тыс.км., t_об- 11 ч. 57 мин. = 43000 сек
Расстояние от Земли до Юпитера 600 млн. км. или 2000 свет.сек. V движения по орбите 26,5 км/с, тогда

DV_x= cosA•6,28•26,5 км/с•2000 сек / 43020 сек

V_x= sinA26,5 км/с + cosA7,7 км/с, тогда как расчетная V_x= sinA26,5 км/с

Эту разницу ( cosA7,7 м/с)между расчетной и измеренной скоростью легко установить. Но у меня нет данных для Амальтеи, а есть для Сириуса.

Сириус - самая яркая звезда на небе. У Сириуса А есть спутник Сириус В. Период обращения 50 лет. Расстояние до Сириуса 8,5 световых лет. Скорость движения центра вращения относительно Солнца Vох = -7,6 км/с. Знак (-) означает, что мы сближаемся. Измеряемая лучевая скорость с учетом поправочной должна быть:



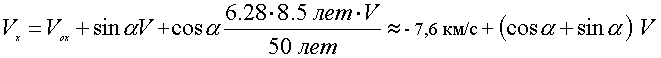
Наблюдаем ли мы это смещение ( cosA+ sinA) V . Несомненно, так как звезды имеют разный спектральный класс, достаточно точно можно определять лучевые скорости каждого из компонентов двойной системы, но орбита движения спутника Сириуса В вокруг Сириуса А не является окружностью, как в случае с Амальтеей, а является элипсом с примерным соотношением полуосей как 2:1. Предлагаю для удобства анализа воспользоваться преобразованиями Галилея и построить кривую изменения лучевых скоростей, для этого найдем орбиту, по которой должно было бы двигаться тело, если скорость излучения относительно наблюдателя в разные моменты времени принимать за const, для этого найдем точки, в которых находилась бы звезда, если бы она продолжала движение в пространстве в течение времени, за которое свет идет до нас, с той же скоростью и направлением, с каким двигалась в пространстве относительно нас в момент излучения света, воспринимаемого нами в данный момент.

Рисунок I



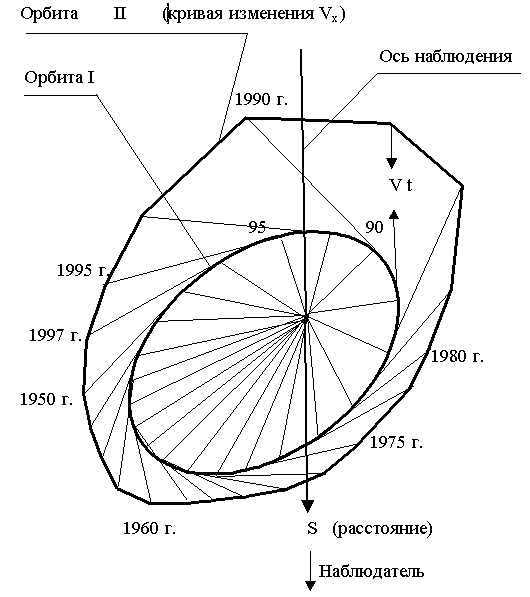
Итак: при наблюдении движения спутника мы должны наблюдать, что изменения положения относительно оси y и z происходят так, как это происходило в действительности (орбита I), а лучевая скорость должна изменяться так, как если бы спутник двигался по орбите II, так ли это можно проверить сравнивая положение спутника по оси y и измеренную Vх (лучевую скорость).

Таблица измерения лучевой скорости.

Дата	Сириус А	Сириус В	Vx относ. орбиты
1950.06	- 5.4	-12.0	- 6.6
1952.57	- 6.3	- 10.0	- 3.7
1955.07	- 7.0	- 8.8	- 1.8
1957.58	- 7.4	- 7.7	+ 0.3
1960.08	- 7.8	- 7.1	+ 0.7
1963.42	- 8.2	- 6.4	+ 1.8
1965.93	- 8.4	- 5.9	+ 2.5
1969.26	- 8.7	- 5.4	+ 3.3
1971.78	- 8.9	- 5.0	+ 3.9
1975.11	- 9.0	- 4.7	+ 4.3
1978.45	- 9.2	- 4.4	+ 4.8
1981.79	- 9.2	- 4.4	+ 4.8
1985.13	- 9.1	- 4.6	+ 4.5
1988.05	- 8.8	- 5.3	+ 3.5
1990.97	- 7.5	- 7.8	- 0.3
1993.06	- 5.1	- 12.7	- 7.6
1995.56	- 2.8	- 18.0	- 15.2
1997.65	- 4.0	- 14.8	- 10.8
1999.74	- 5.2	- 12.3	- 7.1