Случай, когда E>0 соответствует e>1 - гипербола; E=0 означает, что e=1 - парабола; E < 0 соответствует e < 1, - а это эллипс. Но есть и предельный случай, когда E = - mα2/2M2, что соответствует e=0 и круговой траектории.
В случае эллиптической траектории имеем
rmin= p/(1+e) и rmax= p/(1-e)
Следовательно, большая полуось -  , малая полуось - , малая полуось -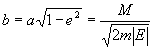
Исходя из закона сохранения момента импульса, а именно, из постоянства скорости заметаемой площади (формула (4)) можно подсчитать площадь эллипса: φ = M/2m , но за период T будет заметена вся площадь, следовательно S = MT/2m. С другой стороны, площадь эллипса равна S = π ab. Откуда период может быть выражен как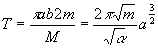 , что в точности соответствует третьему закону Кеплера. , что в точности соответствует третьему закону Кеплера.
Что касается получения зависимостей координат от времени, то, хотя они и представляют собой периодические функции, этот вопрос не совсем тривиален. Так, если выбрать параметр 0£M<2π, связанный со временем как M = M0±2π k×t / T, где за счет целого k обеспечивается область определения [0,2π), то после интегрирования путем замены переменных получается, что
M = Θ - e sin Θ (9)
где Θ - некоторый параметр, принадлежащий диапазону [0,2π). Легко видеть, что полученное уравнение (9) трансцендентно относительно функции Θ (M). Однако использовать (9) необходимо, так как величина M связана со временем линейно, а из Θ легко вычисляются координаты:
x = α(cosΘ-e),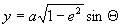 . .
И, соответственно,
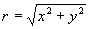 , φ = arctg(y/x). , φ = arctg(y/x).
Получение численного решения уравнения (9) любой необходимой точности в настоящее время труда не представляет. Но до появления компьютеров астрономам часто приходилось затрачивать много усилий на вычисления и публикацию соответствующих таблиц. Интересно, что эта "традиция" продолжает сохраняться в нашей стране по сегодняшний день.
Можно ли из сказанного сделать какие-либо дополнительные выводы? - Да, можно. В первую очередь, следует проанализировать, к каким изменениям может привести отличие гравитационного потенциала от U = -a/ r. Отклонения удобно анализировать и часто рассматриваются в виде U = -a/ rb, так как любые малые изменения представимы как первый член разложения ряда, а на больших расстояниях выполняется условие нормировки U(¥)=0. Легко видеть, что 0 << FONT FACE=symbol>b, иначе мы имеем расходимость на больших расстояниях. Также бессмысленно рассматриватьb>2, потому что в этом случае при сближении тел падение неизбежно (так как потенциал притяжения превосходит центробежный потенциал). Конечно, главный интерес представляют собой связанные состояния, так как на примере солнечной системы легко сопоставить полученные выводы с точно измеренными данными. В случае, когдаbнезначительно отличается от единицы, легко показать, что Кеплеровские эллиптические орбиты становятся незамкнутыми, а угол смещения перигелия за один оборот прямо пропорционален величине этого отличия:
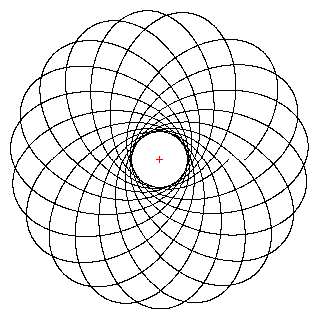 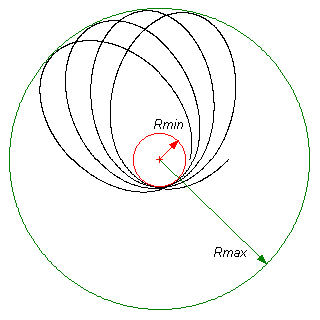
Однако наличие величин максимального удаления и минимального сближения (это определяется только видом Ueff) остается верным при любых изменениях.
Долговременные наблюдения планет позволяют сделать однозначный вывод:b≡ 1, так как все возмущения носят гармонический характер (только периодические) и связаны с взаимным влиянием объектов солнечной системы друг на друга. Исключение составляет орбита только ближайшей к Солнцу планеты - Меркурия, регулярное смещение перигелия которого связано с эффектом нелинейного искривления пространства-времени вблизи тяжелого тела, что точно соответствует выводам общей теории относительности. Возможное замыкание траекторий носит чисто случайный характер и неустойчиво:
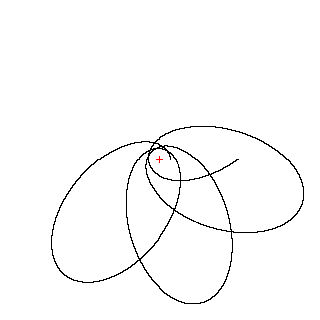 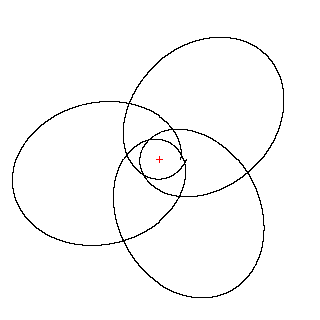
В случаеb®2 снизу проявляется очень интересный эффект (обнаружен при компьютерном моделировании студентами МГУ): тело все большую и большую долю времени начинает проводить вблизи границ (т.е. вблизи Rminи Rmax), а переходы становятся достаточно быстрыми:
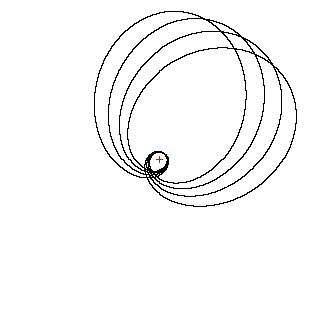 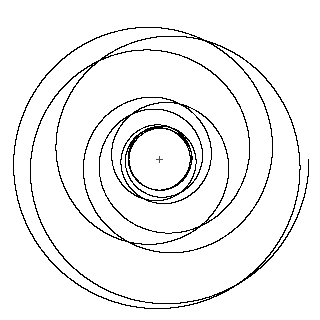
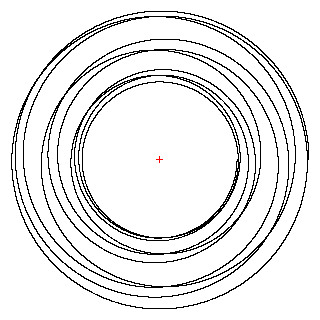 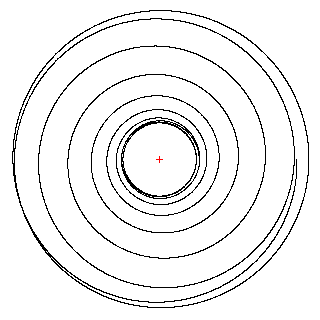
Однако надо заметить, что подобрать параметры, соответствующие связанному состоянию, в этом случае достаточно трудно.
Автор: С.А.Астахов - физик |



